O desvio padrão é uma ferramenta estatística poderosa que ajuda a entender a variabilidade dos dados. Em termos simples, ele mede o quanto os dados de um conjunto estão espalhados em relação à média. Se você está se perguntando como calcular o desvio padrão e como ele pode ser útil no seu dia a dia, este texto vai te guiar de forma clara e simples.
O Que É o Desvio Padrão?
Para entender o desvio padrão, imagine que você está medindo a altura de um grupo de pessoas. Se todos têm alturas muito semelhantes, o desvio padrão será pequeno, indicando pouca variação. Se as alturas variam muito, o desvio padrão será grande, mostrando uma grande dispersão.
Como Calcular o Desvio Padrão
Vamos simplificar o cálculo do desvio padrão com um exemplo passo a passo. Suponha que você tem os seguintes cinco números: 4, 8, 6, 5 e 7. Aqui está como você calcula o desvio padrão:
1. Calcule a Média: Primeiro, você precisa encontrar a média dos números. A média é a soma de todos os números dividida pelo total de números.
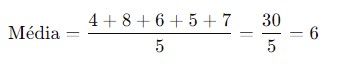
2. Subtraia a Média e Eleve ao Quadrado: Para cada número, subtraia a média e eleve o resultado ao quadrado.
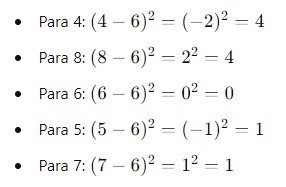
3. Calcule a Média dos Valores Ao Quadrado: Some todos os valores obtidos e divida pelo número total de observações. Este é o “variância”.
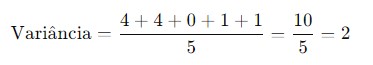
4. Tire a Raiz Quadrada da Variância: Finalmente, tire a raiz quadrada da variância para obter o desvio padrão.
![]()
Então, o desvio padrão para este conjunto de dados é aproximadamente 1,41.
Principais Aplicações do Desvio Padrão
O desvio padrão tem várias aplicações práticas em diferentes áreas. Aqui estão algumas das mais importantes:
- Educação: Em escolas e universidades, o desvio padrão é usado para analisar a distribuição das notas dos alunos. Um desvio padrão baixo pode indicar que a maioria dos alunos obteve notas semelhantes, enquanto um desvio padrão alto pode sugerir uma grande variação nas notas.
- Finanças: No mercado financeiro, o desvio padrão é usado para medir a volatilidade dos preços das ações. Investidores utilizam essa medida para avaliar o risco associado a diferentes investimentos. Um desvio padrão maior indica maior risco, pois os preços das ações variam mais.
- Qualidade de Produção: Em fábricas e indústrias, o desvio padrão é utilizado para monitorar a qualidade dos produtos. Por exemplo, se uma linha de produção fabrica parafusos, um desvio padrão pequeno nas medidas dos parafusos indica que eles são consistentes e de alta qualidade.
- Pesquisa Científica: Em pesquisas e experimentos, o desvio padrão ajuda os cientistas a entender a variabilidade dos dados e a confiabilidade dos resultados. Se os dados de um experimento têm um desvio padrão baixo, os resultados são mais consistentes.
- Saúde: No campo da saúde, o desvio padrão é utilizado para analisar dados de estudos clínicos, como a variação na eficácia de um medicamento entre diferentes pacientes. Isso ajuda a determinar se um tratamento é consistentemente eficaz ou se a resposta varia amplamente entre os indivíduos.
Conclusão
O desvio padrão é uma ferramenta essencial para entender e interpretar a variabilidade dos dados. Com um cálculo simples, você pode obter uma medida que revela muito sobre a dispersão dos números em um conjunto de dados. Seja em finanças, educação, produção ou pesquisa científica, entender e aplicar o desvio padrão pode oferecer insights valiosos e melhorar a tomada de decisões. Com essa base, você pode começar a aplicar o conceito em várias áreas e ver como ele pode facilitar a análise de dados no seu cotidiano.
Para outros textos relacionados a finanças e economia acesse nosso menu para mais informações.
Qualquer dúvida ou sugestão, deixe seu comentário nos campos abaixo.
Deixe um comentário